Profil
Recent engineering problems become more and more complex, nonlinear and high-dimensional. We develop together with students systems to analyze, simulate and control these technological processes. Control algorithms like Model Predictive Control and fresh high-level programming languages like Julia or MATLAB are associated with artificial intelligence, embedded computing or process engineering to span a wide range of research. These fields of research are explained in detail below.
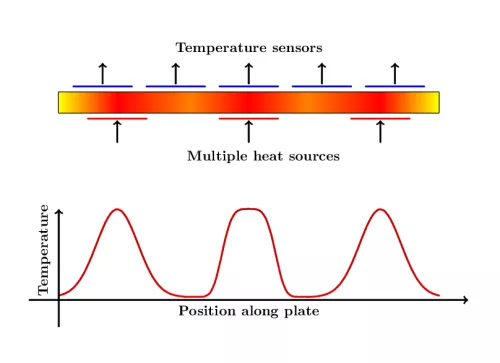
Thermal Process Engineering
Thermal problems play an important role in many technological processes. Many examples like building air conditioning, cooling of engines or server clusters, and optimal tempering for the production of synthetic material unveil the significance of the right heat supply. Our team develops simulations and control algorithms for thermal problems in the case of multiple heat sources. In these scenarios the controller has to decide how much heat shall be supplied and at which position. Common applications can be found in the field of bake processes for the semiconductor industry.
Scientific Machine Learning
Recent machine learning approaches have a huge impact on IT services like search engines and social networks. Though, the research of complex systems bases as well on data-driven modeling. In many cases it is too complicated to describe these complex systems in detail. Therefore, systems with partly known properties are modeled as so called grey box models to approach the real system with the computation on large data sets. For example the driving dynamics of vehicles cannot be described in detail because every component has some certain influence. Instead a grey box model is considered which is improved with data from experiments and test drives. Chemical reactions with a huge amount of particles or reactants state another example. It is very hard to state a model in closed form for these reactions because every component could interact with each other. Thus, these chemical reactions are modeled as grey box models and optimized with data from experiments.
See also: SciML
Embedded Systems
Embedded systems can be found in almost every technological application ranging from consumer electronics to industrial robotics. They are used for measuring and processing data, for example light management in buildings. In many cases, commercial controllers are less flexible and more expensive than single-board computer. Thus, we use single-board computers as controlling units in scientific projects and small scale industrial processes in the areas of process technology, electrical and mechanical engineering to examine their field of application.
Thermal Processes
We develop three-dimensional numerical models of heating plates with multiple sources. The operating heat conduction is assumed as a quasi-linear process to enable the analysis of high temperature processes on a very precise level. We model actuators and sensors with characteristics (e.g. imperfections) which are situated on the plate’s boundaries.
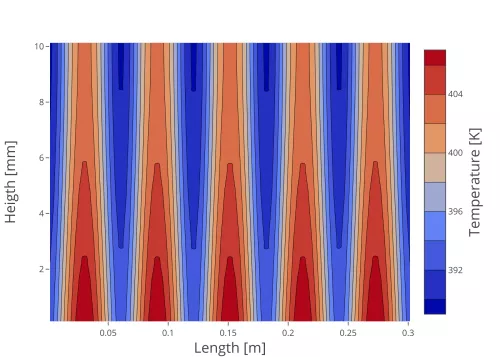
Stage 1: Prototype of model
In the first part of this project a two-dimensional prototype of a quasi-linear heat conduction model was created to highlight the main problems and goals of this project.
- Analytical modeling of quasi-linear heat conduction
- Description of measuring and actuation along boundaries
- Numerical modeling with Finite Volumes
- Simulation, evaluation and discussion of resulting heat conduction
Article and Source Code
- S. Scholz, L. Berger: Modeling of a multiple source heating plate. arxiv:2011.14939
- GitHub: MultipleSourceHeatingPlate2D.jl
Stage 2: A digital twin
In the second stage a software library shall be developed to simulate quasi-linear heat conduction in one, two and three dimensions. Furthermore, the basic control and machine learning concepts shall be sketched. This is still work in progress!
Development of a software library to simulate quasi-linear heat conduction
Documentation and introducing tutorials
Design of the open-loop and closed-loop control
Design of scientific machine learning methods
Source Code
- GitHub: Hestia.jl
Theses and Projects
We offer theses and projects in the domain of modeling, simulation and control. A selection of finished projects and theses can be found here.
Scientific computing for multi-dimensional nonlinear heat conduction and control of multiple heat sources
Abstract
As part of this work, the author developed the two software packages "Hestia.jl" and "BellBruno.jl" in the Julia programming language and made them freely available. We use "Hestia.jl" to create thermal models in code as differential equations and "BellBruno.jl" to calculate the derivatives of the reference signal for the flatness-based control.
PhD Thesis (2025) in English
https://oparu.uni-ulm.de/items/5e76b0c7-b462-43cb-9ca8-7709480b9566
Model Predictive Control for Cascaded Electrical Oscillators
Abstract
This project aims to implement a model predictive control on a system with Nth-order RLC circuits connected in cascade. It treats the implementation and simulation in Matlab, provides a brief explanation of the state space model of the simulated system, and discusses the implementation of the MPC in the programming language C/C++.
Seminar Report (Embedded Control 2025) in English
Simulation of 2-dimensional Heat Conduction with Physics-Informed Neural Networks
Abstract
Heat conduction is a fundamental process that affects countless aspects of our daily lives, from how we heat our homes to the efficiency of industrial systems. In this thesis, I explore an innovative approach to simulating two-dimensional heat conduction using Physics-Informed Neural Networks (PINNs).I begin by laying the groundwork in heat conduction principles, explaining the key concepts and the importance of boundary conditions which will be relevant to this thesis. As I delve into how neural networks can solve differential equations, I highlight the training process and techniques that improve model performance, making these advanced concepts approachable.
The heart of this work is a PINN framework that incorporates the laws of physics directly into the neural network design. This ensures that the simulations adhere closely to the governing equations of heat conduction. Through engaging case studies, I evaluate the effectiveness of this approach, testing it under various heat sources and boundary conditions.The results are promising: not only does this method accurately capture heat distribution, but it also emerges as a strong alternative to traditional techniques like the Finite Difference Method (FDM) and Finite Element Method (FEM). These findings underscore the potential of PINNs to enhance computational efficiency and flexibility, opening doors for future research in more complex thermal systems.In summary, this thesis adds to the growing dialogue between machine learning and engineering, offering valuable insights into how we can harness the power of PINNs to tackle practical heat conduction challenges. I hope this work inspires further exploration in this exciting intersection of fields.
Bachelor Thesis (2024) in English
Parameter Identification of Controlled Heat Conduction
Abstract
This thesis focuses on investigating the identification of parameters in controlled heat conduction within one-dimensional rods. The main focus is on estimating thermal conductivity and controller gain through the utilization of open-loop and closed-loop systems. A proportional controller (P-Controller) is utilized in the closed-loop setup to achieve target temperatures.
The methodology involves solving the forward problem to model heat conduction and solving the inverse problem to estimate the parameters. Three optimization techniques, specifically Nelder-Mead, Conjugate Gradient, and Newton’s Method, are utilized for this purpose. To address system noise, Gaussian noise is introduced to replicate real-world industrial conditions, contrasting with noiseless, idealized simulations. The study compares various sensor configurations to determine the necessary number of sensors to accurately determine , particularly in the presence of noise.
The findings indicate that increasing the number of sensors and implementing suitable optimization techniques significantly improves estimation accuracy in noisy environments. This study provides valuable insights into sensor placement and optimization techniques, making the proposed methodology highly applicable for improving the accuracy and efficiency of industrial heat conduction systems.
Bachelor Thesis (2024) in English
In-Domain Control of a 1-Dimensional Heat Equation
Abstract
Accurate control of heating processes remains an ongoing topic of research due to the wide variety of applications in the process, semiconductor and manufacturing industries. This report investigates the in-domain control of the average temperature in a one dimensional, insulated rod using multiple heat sources.
To this end, the heat diffusion in the rod is modelled by the heat equation which is a partial differential equation. The report introduces a method to spatially discretize the system to obtain a finite dimensional state-space representation in the form of a linear system of ODEs. This model is used to design an LQR feedback controller and a feedforward controller.
The control algorithm is implemented in C-Code and incorporated into a simulation environment by compiling it to a MATLAB executable file in order to increase the computational efficiency and to perform Software-in-the-Loop tests.
Simulations are performed to investigate the open- and closed-loop behavior of the system. The controller is able to track a variety of different reference inputs as long as the bandwidth of the reference is limited and a tracking error is acceptable. Future research directions include the use of output feedback to improve tracking and disturbance rejection as well as methods from optimal control like Model Predictive Control to take constraints of the heat sources into account.
Seminar Report (Embedded Control 2024) in English
Optimization Based Control of Cascaded Electrical Circuits
Abstract
In this thesis, the challenges of optimizing higher-order circuits are addressed, with a focus on various methods to align system performance with desired reference outputs. The primary question under consideration pertains to the feasibility of optimization techniques in managing the complexities of higher-order system dynamics and, if so, which optimization approach—global or local—minimizes output errors.
Three optimization techniques - Flatness-Based Control (FBC), Optimization-Based Control (OBC), and Model Predictive Control (MPC) - are applied and analyzed. Notably, FBC faced challenges when dealing
with higher-order systems, primarily due to its reliance on the steepness of the reference signal. In contrast, OBC and MPC proved effective in handling such systems.
Within the OBC framework, the Polyopt optimizer demonstrated exceptional performance, effectively managing parameter variations. In the context of MPC, the interplay of prediction horizon and control horizon underscored the importance of an extended prediction horizon and a shorter control horizon.
Furthermore, the behavior of global optimizers revealed their ability to closely follow reference signals, albeit with increased jitter. Local optimization, on the other hand, yielded input signals that led to lower errors and smoother output responses.
The findings presented here hold substantial promise for applications in power electronics and motor control, offering the potential for smoother responses and improved control methods, particularly in systems such as, power converters, clippers and clampers.
Master thesis in English
Solution of Maxwell’s Equation - A Numerical Approximation
The objective of this thesis is to provide a comprehensive understanding of Maxwell’s equations and their numerical approximation using the finite-difference time-domain (FDTD) method.
Bachelor Thesis in English
Evaluation of Dynamic Mode Decomposition for Cascaded Electrical Oscillators
In this report the author presents the modeling, implementation and simulation of dynamic mode decomposition for cascaded electrical circuits in open-loop and closed-loop scenarios with full-state feedback.
Report (Scientific Project) in English
Sliding-Mode Control for Nonlinear RC and RLC Circuits
In this report the authors present the design, implementation and simulation of sliding-mode control for small linear and nonlinear electrical circuits.
Report (Embedded Control 2022 / 2023) in English
Simulation of two-dimensional heat conduction in Julia programming language using CUDA
Abstract
Heat is vital when work and energy are involved in phase transitions, according to this fact, heat conduction qualities as well as the properties of molecules inside the bodies needed to be analyzed. Computation of heat transfer has been a considerable challenge during the last decade, especially when time is considered as a component with an unaffordable price.
The heat equation is a parabolic partial differential equation that represents how temperature varies in space over time. It may also be described as the process which reflects how heat is transferring from a higher temperature median to a lower temperature one. In some complex occasions it is nearly impossible to calculate the heat diffusion manually, that is why Julia programming language is utilized to solve one and two-dimensional heat equation problems by using CUDA, which is configured to accelerate the calculation through the graphics processing unit (GPU).
Bachelor thesis in English
High-order electrical RLC oscillators - PID and LQR control
Abstract
The interest of this work is to design a PID and LQR controller for a high-order electrical RLC oscillator. For this purpose, state space equations are first formed for the cases n = 1, n = 2, n = 3 and n = n. After that, the general stability behaviour is checked and simulated. Finally, the PID and LQR controls are created.
Report (Embedded Control 2021 / 2022) in English
Regelungsentwurf mittels maschinellen Lernens für ein Wärmeleitermodell
Abstract
This thesis deals with a one dimensional heat conduction problem: the end of a rod is heated to a given temperature. This process is controlled by a PI controller. Different boundary conditions for the end of the rod are considered. Requirements for the control as well as the parametrization for the different boundary conditions are discussed.
Afterwards the process is simulated numerically using the Julia programming language. Therefore the instationary heat conduction equation is firstly solved manually using the numerical finite difference method FTCS (Forward-Time Central-Space) and after that the vertical line method in connection with generic solvers is used.
The previously used explicit Euler-method is compared with selected Julia solvers. A data set is created that contains the temperature distribution of the different sections of the rod during heating. After that the collected temperature distributions are used to identify through the application of machine learning the control parameters that the PI controller has used during heating. Different optimization algorithms are compared. In addition it is examined how much information, i.e. the temperature distribution of how many location points is needed to reliably identify the parameters.
Bachelor thesis in German
Optimal Control of the heat equation in Julia
Abstract
Optimal control of systems described using partial differential equations is a field of interest in research and industry. The heat equation, a partial differential equation, describes various heating and cooling processes. It is usually accompanied by constraints on the input signals, temperature through the body or both, which motivates applying optimal control in such processes.
In this thesis, a solution to the optimal boundary control of the heat equation is presented. The heat equation is numerically approximated using Finite difference method. The optimal control problem is formulated using a direct method into a non linear program. JuMP, a mathematical modelling language built on Julia is used to solve the problem. Simulation results are presented for a one dimensional rod and a two dimensional plate.
Bachelor thesis in English
Entwicklung einer KI-basierten Lösung zur Temperaturregelung eines Wasserbeckens
Abstract
In dieser Bachelorarbeit wird die Anwendung von Künstliche Intelligenz (KI) in der Regelungstechnik untersucht, wobei der Fokus auf der Entwicklung und Implementierung von KI-basierten Reglern für die Temperaturregelung eines Wasserbeckens liegt. Das Ziel ist es, das Potenzial des Maschinellen Lernens zur effizienten Bewältigung einfacher Regelungsaufgaben zu erforschen. Im Rahmen der Arbeit werden zwei KI-basierte Regler entwickelt:
- Ein Regler, der aus einem Long Short-Term Memory (LSTM) besteht und darauf trainiert wird, das Verhalten eines vorher entwickelten Proportional-Integral-Derivative (PID)-Reglers zu erlernen und nachzuahmen.
- Ein Model Predictive Control (MPC)-Regler welcher als Vorhersagemodell ein Feedforward Neural Network (FFNN) nutzt. Dieses Netzwerk wird darauf
trainiert, das Systemverhalten auf Basis von historischen Betriebsdaten vorherzusagen.
Die Arbeit dokumentiert die Schritte von der Konzeption über die Implementierung bis hin zu Tests und Bewertung der entwickelten Regler. Zur Bewertung der Regler
werden diese mit einem herkömmlichen PID-Regler sowie einem konventionellen MPC-Regler verglichen, die ebenfalls im Rahmen dieser Arbeit entwickelt werden. Die Ergebnisse zeigen, dass die KI-basierten Regler in der Lage sind, die Temperatur des Wasserbeckens mit nur geringfügig schlechterer Leistung als konventionelle Regler zu regeln. Insbesondere der MPC-Regler, der ein datengetriebenes Vorhersagemodell verwendet, zeigt Potenzial für zukünftige Anwendungen, bei denen das Systemverhalten nicht vollständig bekannt ist. Allerdings bringen die KI-basierten Ansätze auch neue Herausforderungen mit sich, wie in dieser Arbeit aufgezeigt wird. Dazu gehören hohe Anforderungen an die Rechenleistung und die Notwendigkeit einer sorgfältigen Parameterauswahl.
Bachelor thesis in German
Publications
Publications
- S. Scholz, L. Berger: Optimization-based Reference Tracking for Two-Dimensional Multiple Source Heating. in Proceedings of 63rd IEEE Conference on Decision and Control. https://ieeexplore.ieee.org/abstract/document/10886335. 2024.
- S. Scholz, C. Bonenberger, N. Scheiter, L. Berger: Simulation and Control of 2-Dimensional Anisotropic Heat Conduction. ASIM SST 2024 Proceedings
- C. Bonenberger, S. Scholz, N. Scheiter: Data-adaptive dynamic simulation via structured Dynamic Mode Decomposition. ASIM SST 2024 Proceedings
- S. Scholz, L. Berger: Optimization-based Trajectory Planning for Heat Conduction. Proceedings of the 2024 25th International Carpathian Control Conference (ICCC), Krynica-Zdrój, Poland, 2024.
- S. Scholz, L. Berger: Fast Computation of Function Composition Derivatives for Flatness-based Control of Diffusion Problems. Journal of Mathematics in Industry 14(1), 2024, 15.
- D. Peters, S. Scholz, L. Berger: Dynamic Mode Decomposition for Cascaded Electrical Circuits. Proceedings of the 2023 6th International Conference on Mathematics and Statistics.
- S. Scholz, L. Berger, D. Lebiedz: Benchmarking of flatness-based controlof the heat equation.
- S. Scholz, L. Berger: Hestia.jl: A Julia library for heat conduction modeling with boundary actuation.
- S. Scholz, L. Berger: Modeling of a multiple source heating plate. arxiv:2011.14939. 2020.
- L. Berger, J. Kretz, D. Beyer, A. Schwersenz: Charged-Particle Lithography. https://doi.org/10.1002/9783527628155.nanotech024. Nanotechnology. Wiley‐VCH. 2010.
- L. Berger, P. Dress, S.H. Yang, C.H. Kuo: Qualification of design-optimized multi-zone hotplate for 45nm node mask making.
SPIE Proceedings 2007. - L. Berger, P. Dress, T.M. Gairing, C.J. Chen, R.G. Hsieh, H.C. Lee, H.C. Hsieh (TSMC): Global critical dimension uniformity improvement for mask fabrication with negative-tone chemically amplified resists by zone-controlled postexposure bake.
Journal of Micro/Nanolithography, MEMS, and MOEMS 2004.
Presentations
Conferences
- Stephan Scholz: Optimization-based Trajectory Planning for Heat Conduction. 25th International Carpathian Control Conference (ICCC), Krynica-Zdrój, Poland, 2024.
- Stephan Scholz: Electrical Circuit Models for Courses on Simulation and Control of Differential Equations - From Transfer Functions to PDEs. DMV Jahrestagung 2023, Ilmenau.
- Stephan Scholz: Fast Computation of Function Composition Derivatives for Flatness-based Control of Diffusion Problems. ECMI 2023, Wroclaw.
- Stephan Scholz: Hestia.jl: A Julia library for heat conduction modeling with boundary actuation. ASIM 2022, Vienna.
Miscellaneous
- Stephan Scholz: Control the Heat: Flatness vs. Optimization. Tag der Promotion 2023, RWU, Weingarten.
- Stephan Scholz: Scientific Machine Learning. Erasmus+ stay 2022, University of Zielona Góra.
- Stephan Scholz: Heating a cuboid is the future of thermal process engineering. Tag der Promotion 2022, RWU, Weingarten.
- Stephan Scholz: Scientific Machine Learning. Kolloquium 2022, RWU, Weingarten.
Scientific Machine Learning
| Date | 30.06.2022 |
| Place | RWU |
Kontakt & Personen
Allgemeine Kontaktinformationen
| Besuchsadresse |
Gebäude H (Hauptgebäude)
Doggenriedstraße
88250 Weingarten |
|---|---|
| Postadresse |
RWU Hochschule Ravensburg-Weingarten University of Applied Sciences Control and Process Engineering Postfach 30 22
D 88216 Weingarten |
Research Group

